数据结构:图
这篇文文章主要介绍一种比较复杂的数据结构–图。主要内容:
- 图的概念及术语
- 图的结构
- 图的遍历
- 深度优先遍历
- 广度优先遍历
图的概念及术语
定义
定义:由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V, E)。其中 G 表示图,V 是图中顶点的集合,E 是图 G 中边的集合。
一些术语
图的术语非常多,其它的术语当用到的时候再去了解。这里介绍几个比较常见的术语:
顶点:表示图中的一个结点。
边:顶点和顶点之间的连线。若连线无方向则为无向边,反之则为有向边,也称为弧。
权:边有与之相关的数值,这个数值称为权。
相邻顶点:由一条边连接在一起的顶点。
度:相邻顶点的数量。指向其它顶点的数量称为出度, 其它顶点指向自己的数量称为入度。
无向图:图中任意两个顶点之间的边都是无向边。
有向图:图中任意两个顶点之间的边都是有向边。
无权图:图中的边是没有任何意义,无权重。
带权图:图中的边有一定的权重。
连通图:图中任意两个顶点都是连通的。
结构
散列表
散列表的具体概念这里就不多介绍了,大部分的语言中都提供了散列表的实现。在 Swift 中,散列表的实现就是字典。
我们可以用散列表来实现一个图结构。
邻接矩阵
两个数组来表示图结构。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存出图中的边或弧的信息。
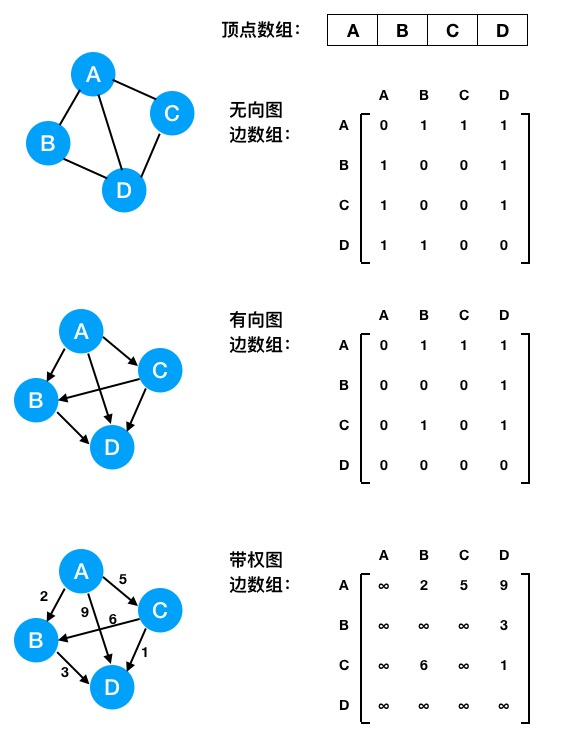
图中展示了三种图的邻接矩阵表示方式。其中:
数字为 0 或者 ∞ 的代表两个顶点之间没有连线,其它数字都代表有连线。在有向图中,数字 1 代表纵向对应顶点指向横向对应顶点。在带权图中,数字的数值大小则代表这条边的权。
图的定义:
1 | class Graph { |
邻接表
数组和链表结合来表示图结构。一个一维数组存储图中顶点信息,链表则用来表示与某个顶点相邻的顶点。
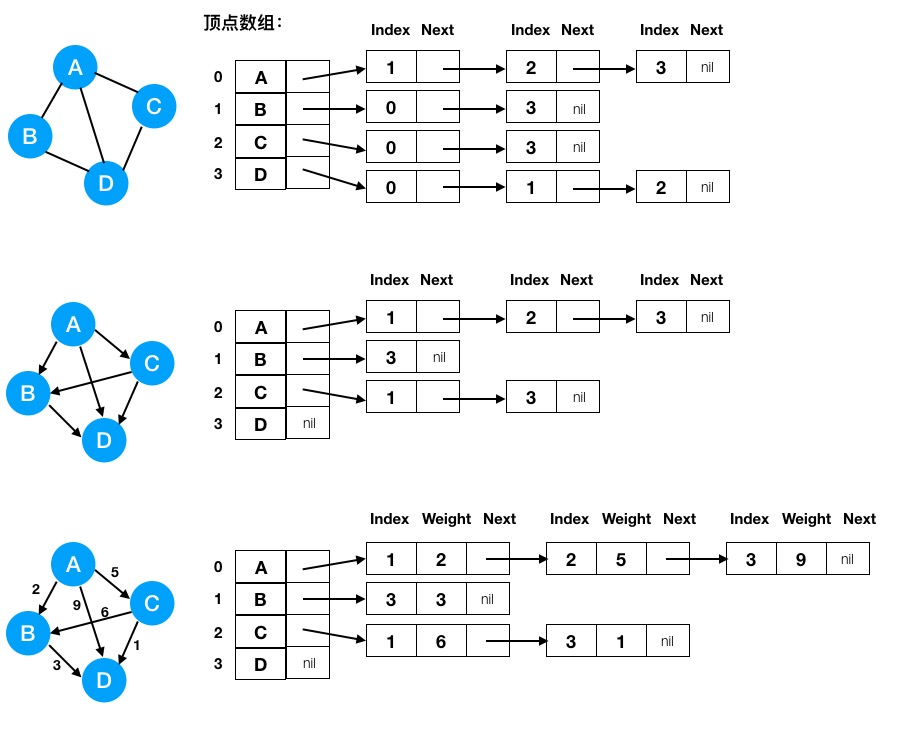
图中展示了三种图的邻接矩阵表示方式。其中:
链表结点的 index 指向数组中与自己相邻顶点的下标,next 指向下一个与自己相邻的顶点,最后一个顶点 next 置为 nil。在带权图中,对链表结点的定义扩充了一个 Weight 控件,表示这条边的权重。
图的定义:
1 | // 图顶点 |
边集数组
边集数组是由两个一维数组构成。一个是存储顶点信息的,另一个存储边的信息。边数组中每个数据元素都由 begin(起点下标),end(终点下标),weight(权) 组成。
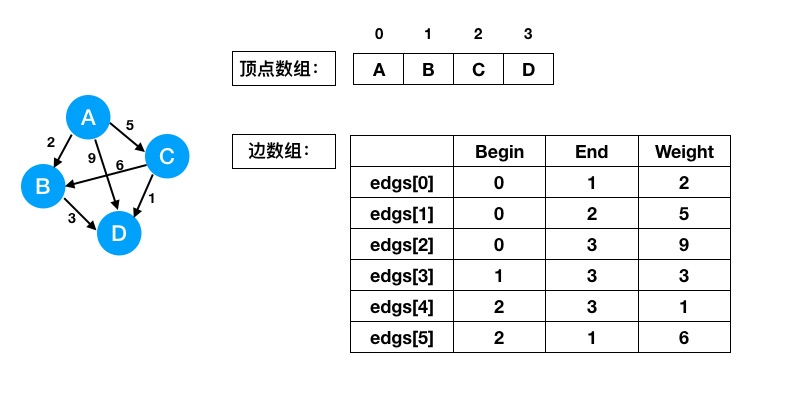
边集数组因为其存储形式,比较适合存储有向图及带权图。若存储无向图,则对同一条边需要两个数据元素来存储,对空间会造成比较大的浪费。
图的定义:
1 | class Edge { |
遍历
准备工作
这里我们是利用前面散列表来表示图。
1 | var graph = [String: [String]]() |
上面的代码创建了一个下图中的图结构。
广度优先遍历
广度优先遍历类似于树的层序遍历。
从 A 开始,找到所有自己一步能到达的顶点(B,C)加入队列,查找是否是自己需要的(G),如果不是,再将这些顶点(B,C)一步能到达的顶点(D,E),加入到队列中。如果找到,直接返回结果,否则就这样一层一层的找下去,直至队列为空。
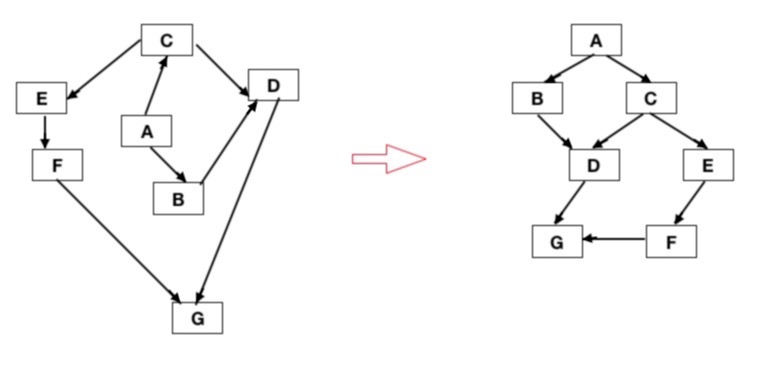
1 | // 存储已访问的顶点 |
深度优先遍历
- 从某个顶点(A)出发,访问顶点并标记为已访问。
- 访问 A 的其中一个邻接点(假设为 B),如果没有访问过,访问该顶点并标记为已访问。
- 然后再访问该顶点(B)的邻接点(D),重复上述步骤。
1 | // 深度优先遍历 |
结论
Depth_First_Search的实现用递归,Breadth_First_Search的实现用循环(配合队列)。