数据结构：二叉树

Posted on 2018-04-18 In 数据结构与算法

这篇文章主要介绍树结构中的一种特殊存在——二叉树。主要内容有：

二叉树的概念
二叉树的基本结构
二叉树的操作

概念

二叉树：每个结点最多有两个子结点，两个子结点是有次序的，且子结点次序不能颠倒。两个子结点一般称之为左结点及右结点。
层次：在树中，节点的层次从根开始定义，根为第一层。
深度：树中节点的最大层次为树的深度。
度：结点拥有的结点数。
分支结点：度不为0的结点。
叶子节点： 度为0的结点。
特殊二叉树
- 满二叉树：所有分支结点都存在左右两节点，并且所有叶子结点都在同一层。
- 斜树：所有的结点都只有左子结点或者右子结点。
- 完全二叉树：对一棵具有n个结点的二叉树按层序编号，如果编号i（1<=i<=n）的结点
  与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则称之为完全二叉树。
- 二叉查找树：左子树中节点的值都小于根节点的值，右子树中节点的值都大于根节点的值。

结构

顺序存储结构

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系。使用顺序存储结构表现二叉树的时候，在其线性结构中，会存在一些空结点，但是其会占据一定的内存空间，会造成存储空间的浪费。

链式存储结构

由于二叉树的每个结点最多有两个孩子，所以为每个结点设计一个数据域和两个指针域。

结点的定义

结点的结构定义：

class TreeNode {
    var value: String
    var left: TreeNode?
    var right: TreeNode?
    
    init(_ value: String) {
        self.value = value
    }
}

操作

创建二叉树

现在我们创建一棵如图所示的二叉树：

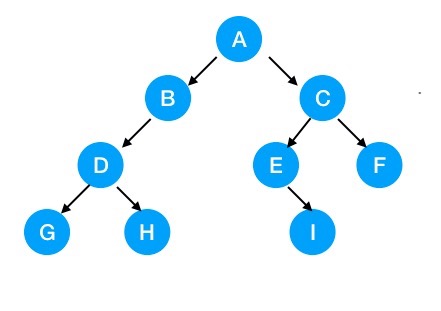
为了能让每个结点确认是否有左右子结点，我们将预期二叉树进行一个扩展：

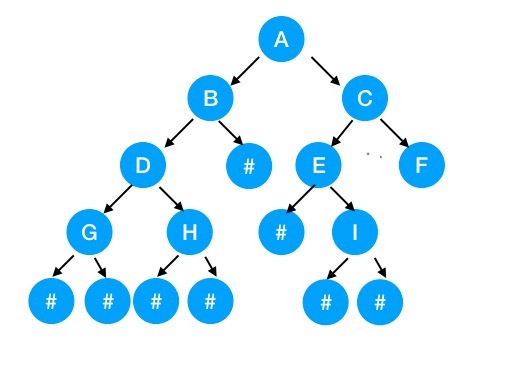
我们给每一个结点的空指针引出一个虚结点，其值为一个特定值——#。

创建这棵二叉树代码：

let arr = ["A", "B", "D", "G", "#", "#", "H", "#", "#", "#", "C", "E", "#", "I", "#", "#", "F"]
var index = 0

func preCreateTree(_ tree: inout BinaryTreeNode?) {
    if index > arr.count-1 {
        return
    }

    let value = arr[index]

    index += 1

    if value == "#" {
        tree = nil
    } else {
        // 生成根结点
        tree = BinaryTreeNode(value)

        // 构造左子树
        preCreateTree(&tree!.leftChild)

        // 构造右子树
        preCreateTree(&tree!.rightChild)
    }
}

var root: BinaryTreeNode? = BinaryTreeNode(nil)

preCreateTree(&root)

遍历

二叉树的遍历主要分为四种：

前序遍历：根结点–>左子树–>右子树。
中序遍历：左子树–>根结点–>右子树。
后序遍历：左子树–>右子树–>根结点。
层序遍历：从上至下一层一层遍历。

前序遍历

前面创建二叉树时，我们有一个数组 [“A”, “B”, “D”, “G”, “#”, “#”, “H”, “#”, “#”, “#”, “C”, “E”, “#”, “I”, “#”, “#”, “F”]，这个数组是如何得到的呢？

就是根据前序遍历扩展二叉树的结果得到的这个数组，并利用这个数组前序创建了我们预期的二叉树。

前序遍历代码：

func preOrderTraverse(_ tree: BinaryTreeNode?) {
    if let node = tree {
        print("value is \(node.value)")

        // 先序遍历左子树
        preOrderTraverse(node.leftChild)

        // 再先序遍历右子树
        preOrderTraverse(node.rightChild)
    }
}

中序遍历

中序遍历代码：

func inOrdertraverse(_ tree: BinaryTreeNode?) {
    if let node = tree {
        // 中序遍历左子树
        inOrdertraverse(node.leftChild)

        print("value is \(node.value)")

        // 中序遍历右子树
        inOrdertraverse(node.rightChild)
    }
}

后序遍历

后序遍历代码：

func lastOrdertraverse(_ tree: BinaryTreeNode?) {
    if let node = tree {
        // 后序遍历左子树
        lastOrdertraverse(node.leftChild)

        // 后序遍历右子树
        lastOrdertraverse(node.rightChild)

        print("value is \(node.value)")
    }
}

层序遍历

层序遍历代码：

func levelOrdertraverse(_ tree: BinaryTreeNode?) {
    guard let root = tree else {
        return
    }
    
    var tempQueue: [BinaryTreeNode] = []
    
    // 将根节点加入数组
    if let _ = root.value {
        tempQueue.insert(root, at: 0)
    }
    
    while tempQueue.count != 0 {
    	  // 取出数组最后一个元素
        let temp = tempQueue.popLast()!
        
        // 将下一层结点依次插入到数组最前面
        if let l = temp.leftChild, l.value != nil {
            tempQueue.insert(l, at: 0)
        }
        
        if let r = temp.rightChild, r.value != nil {
            tempQueue.insert(r, at: 0)
        }
        
        print(temp.value)
    }
}

树的最大深度

func maxDepth(_ tree: BinaryTreeNode?) -> Int {
    guard let root = tree else {
        return 0
    }
    
    return max(maxDepth(root.leftChild), maxDepth(root.rightChild)) + 1
}

推导遍历结果

遍历特点：

前序遍历：根结点–>左子树–>右子树。

中序遍历：左子树–>根结点–>右子树。

后序遍历：左子树–>右子树–>根结点。

根据遍历特点，得出解题思路：

找到根–>找到左右子树
一直重复这个操作，直到最后一个子节点。

题目一：求后序遍历

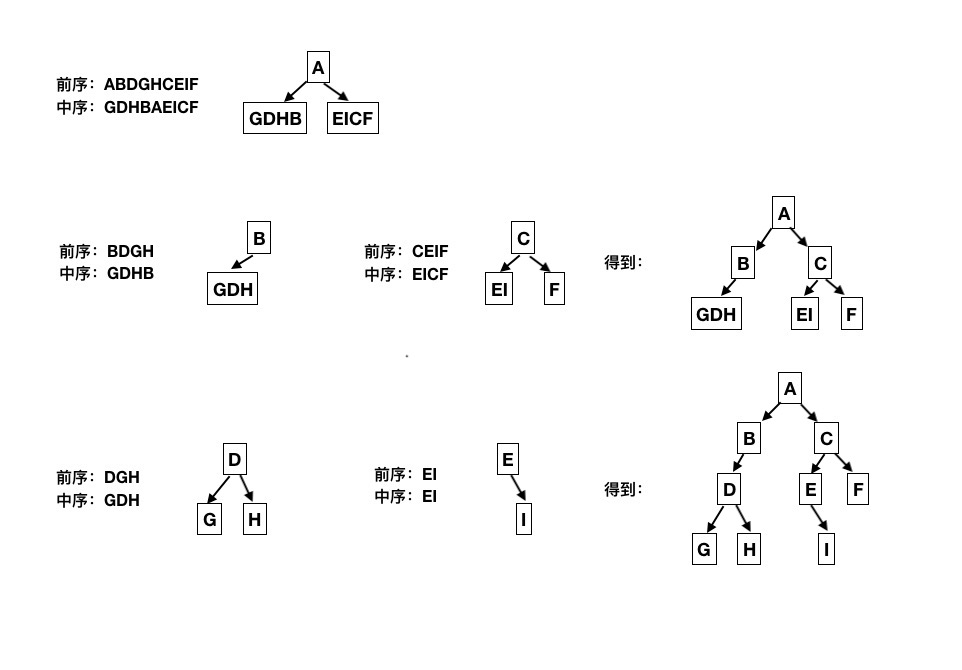
题目：已知前序遍历 ABDGHCEIF 及中序遍历 GDHBAEICF，求出后序遍历顺序？

解答：

先序遍历的结果是ABDGHCEIF，根据先序得到根节点是A；中序遍历的结果是GDHBAEICF，根据中序得到A之前的节点都是左子树，A之后的节点都是右子树。
再对左右子树进行第一步的分析。最终能得到二叉树的完整结构。

题目二：求前序遍历

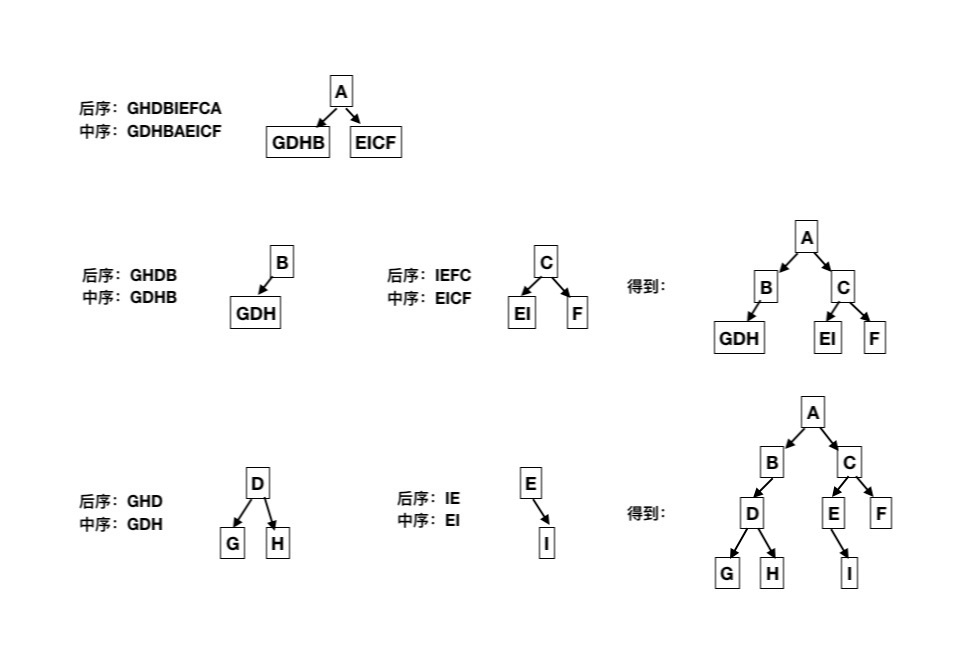
题目：已知后序遍历 GHDBIEFCA 及中序遍历 GDHBAEICF，求出后序遍历顺序？

解答：

后序遍历的结果是GHDBIEFCA，根据先序得到根节点是A；中序遍历的结果是GDHBAEICF，根据中序得到A之前的节点都是左子树，A之后的节点都是右子树。
再对左右子树进行第一步的分析。最终能得到二叉树的完整结构。

总结一下

已知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。

但是，已知前序和后序是不能确定一棵二叉树的。

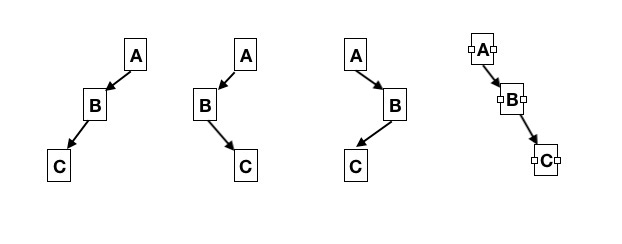
例如：前序遍历序列为 ABC 及后序遍历序列为 CBA。

可以确定 A 一定是根节点，但是接下来无法确定哪些是左子树，哪些是右子树。此时，这棵二叉树有以下四种可能：